|
|
不得不說,有時候無知是福,看到一點有趣而深刻的東東,就能感覺到神奇。越是我們熟悉的東西,往往卻是我們進一步理解深刻的障礙,而之所以是障礙是我們并不知道這個是我們理解問題的障礙。困惑中的每一次豁然開朗往往是從一點一滴的我們已經成為慣性思維中開始。越是深刻的原理,往往越是簡單強大。就像愛因斯坦打破牛頓給我們原有的世界觀一樣。對于一個打破常規,讓你重新理解問題的最簡單的方法就是把你整個思考的前提否定。而帶來的結果就是我們看問題的角度,層面有了更大的擴展。所以,有時候知道的太多反而不美,做一個白癡也很幸福。
哎,又無病呻吟了半天。之所以有上述感想。還得感謝自己的同學。由于我沒有看過MIT的經典課程《算法導論》而被鄙視,而且更無語的是,我的理由是“聽不懂,如果有老師的課堂發音的記錄”,而事實上。這個MIT早就提供了,為了照顧想我這樣的聽力不好的家伙。好吧,我是個白癡,不過就像上面講的,白癡也有白癡的幸福。這個假期,無聊的時候,不僅可以看《愛情公寓2》也可以屢屢自己的數學常識了。:)
《算法導論》是一名研究算法設計的課程。設計算法,我們關心的主要是2個方面,一個是性能,另一個是資源花費。當然,我們重點的是性能,我們總是希望我們的程序跑的更快。那么學習算法到底有什么用呢?這是一個經典的問題。Charles Leiserson 是這樣給我們解答的。首先,列舉了一大堆在實際編程中比性能更重要的東西:可維護性,模塊化,功能,用戶體驗等等。特別是用戶體驗,那么既然有這么多的東東比算法重要,那么為什么我們還要學習算法呢?
- 算法決定了可行還是不可行。
在一些實時的情況下,比如機器人等嵌入式設備,我們不夠快,那么就沒有意義,如果我們用了太多的內存,同樣不行。所以,算法這個東東,總是在我們計算機領域的最前沿部分,如人工智能,搜索引擎,數據挖掘。如果我們是在做10年前就已經實現了的東西,那么性能的確在一些情況下已經不重要了。但是,如果想做一些別人沒有做過的東西,真正的實現從無到有的過程。那么其中遇到的絕大多數問題都是,數據太復雜了。沒有能力在有限的資源下找到答案。這也就是為什么叫計算機科學,而不是計算機工程。(當然科學這個和名字是無關的,比如物理,從來沒有那個學校叫個什么物理科學什么的。:))。不得不說,MIT的目標是為世界培養leader,而我們那破學校是為了培養farmer(這里并沒有不敬在里面,而且事實上,做一個farmer挺好的,每年坐在家里,收個房租,年末村里再分個幾十萬,比那些城里白領好多了在物質上)。其實也不那么絕對,非要改變世界,只要是之前沒有做過的程序,我們在實現之前,首先思考的一定是算法。其次,則是對他不斷的優化,完善。
對絕大多數的剛剛參加工作的同學,往往不能體會到整個產品的創建過程。參與的僅僅是完善,算法的設計或是大體設計已經完成,所以感覺不到算法的存在。而匆匆下了學校白學的定論。而隨著工作時間變長,總會遇到沒有或是不能直接利用原有設計的東東,那么算法也就體現出價值了。
- 算法是一種描述程序行為的通用語言。
我們可以通過算法去描述程序的運行流程,在任何地方。他不僅能在實踐中得到體現,也能在理論中得到證明。而且能夠得到大家一致的看法。而這是別的永遠無法做到的,比如用戶體驗,每個人都有自己的想法,我們不可能讓所有人都滿意我們的設計,而算法卻可以做到,因為快就是快。放到計算機上一跑結果自知。別人無法擊敗你,即便是再挑剔的對手,只要你足夠出色。而能夠滿足這樣條件的前提就是,算法是一個如此一般化,基礎的東西。就像Charles Leiserson 所講,算法就像錢,你可以用錢去買吃的,喝的。而衡量這些花費的就是錢的數目。在計算機上,則是,選擇一個這樣的策略,需要花費多少。選擇另一個策略,需要花費多少。而衡量這2個選擇誰的花費多呢?是算法。
算法在計算機中的地位,就和數學在所有理科學科中的地位一樣。我曾經問過我的數學老師一個問題,他的回答讓我直到現在還記憶猶新。“老師,數學在您眼中是什么呢?”“數學是所有理科中是最奇妙的一個。因為他可以獨立于其他任何學科存在而其他學科離開不了數學。”是的。能夠想象物理化學離開數學之后是什么樣子么?但是數學為什么能夠獨立存在?是因為他構建了一門語言,一門偉大的語言。使用這門語言可以讓知識在任何領域中環繞,學好數學就好像有了一張無限透支的通用支票,可以在任何地方花費(黃金?)。作為一個可以讓這么多地方都通用的原因中最重要的就是,他是超級穩定的。是一個說一不二的世界。一個公平的世界,絕對的世界(當然,現在數學這個概念也不準確了,這個充分體現了哲學思想,有正必有反啊:P)。他所確定的東西的結果是肯定的。沒有歧義,而且不隨時間變化而流動。比如,我們真實世界中交流的語言,比如“忽悠”,“猥瑣”。等等。很多詞義,隨著時間的變化而改變了。使得很多年紀大的人,和我們這年輕人在交流上就產生了隔閡。而我們最熟悉另一個例子就是文言文,特別是其中的一些扭曲的字。但數學這種基礎類學科是不會的。至少在一個可以預見的范圍是穩定的,沒有地域限制的。所以,數學才能站在人類科學發展的最前沿,他的每一次前進的一小步,都能改變世界。這就是數學之美。同樣也是自己能夠讓絕大多數人接受的最大障礙。由于他改變的太慢,而且枯燥。絕大多數人無法深入的理解。當用世俗,腐爛,充滿銅臭,功利的眼光看待純凈的數學世界,必然發現數學無用。而且,這的確是事實,因為大部分人,都不可能成為改變世界的家伙(這里的確不準確,因為改變世界話題太大,修理地球同樣也是改變世界。)。
算法,同樣為我們計算機構建了一個純凈的世界。一個說一不二的世界,他所確定的,沒有能夠反駁的。當然,就和學習數學一樣,我們不是去成為數學家,學習物理,不是去成為物理學家,然后去做哪些能夠改變世界的東西。學習這些基礎類學科的重要在于,他提供了一個讓我們和那些站在人類史上最頂尖的家伙們交流的語言,從我的角度來看。如果沒學好數學,能夠和牛頓,愛因斯坦交流么?沒有學好算法,能夠和高爺爺交流么?作為一個普通人,我們只要學習到他們身上的一點點,也就足夠了。當然,這不是對所有家伙都有效,有些人總是想,和那些老家伙有什么好交流的,給我一個周杰倫的簽名吧。:)
- 學習算法還有一個原因,是的,就是興趣。這個傳說中最牛X的老師。
喜歡算法,沒有別的原因,是的。我就是喜歡比別人快速的感覺。喜歡數學,是的。因為大部分人數學不好。所以我就喜歡數學。迎難而上,哥就是喜歡做別人做不了的東西。是的,雖然聽上去很牽強,而且比較扭曲。比較符合印象中90后的想法。不知道90后是不是能產生更多的數學家呢?
讓我們回到我們的算法上,既然我們這么關注性能,那么什么是影響性能的因素呢?
對于一個計算機外行來說,首先就是計算機硬件本身的運算能力。多一個超級牛的CPU,超大的內存,固態硬盤。肯定運算快。的確,如果你拿一個超級計算機和地攤上買的一個小的計算器比運算能力。這個實在是一個很顯然的結果。是的,所以,我們有些情況下,需要思考在相同條件下,到底哪個算法的性能更高。這比較的是相對速度。但是我們卻不能忘了這一點。有時,我們想使用一些很一般的計算機,通過優秀的算法,來打敗那些擁有更高硬件的那些家伙們,而我們則必須關心算法性能的絕對速度。那么我們該如何描述這些看似互相矛盾的東西呢?不要忘記,算法可是基礎啊,我們要的是一個確切的答案。我們如何給出一個確切的答案,而這個答案不管是超級計算機,還是普通PC都能夠支持呢?這就是算法中最重要的一個概念,甚至是一切分析的大前提,一個可以把這些復雜的因素都考慮在內(或是都不考慮在內)的東東轉換為可以用數學分析的對象。這就是漸進分析。
漸進分析的基本思想是:
- 忽略硬件結構
- 不使用真實世界的運行時間,而是關心運行時間的增長速度為對象
漸進分析是一個非常龐大的概念,我們最熟悉的,也是大多數本科院校教我們的就是Θ,O,Ω等等類似的這些符號。這里只從Θ開始。
對一個初學者,Θ-notation是比較容易接受的。對一個多項式,我們只需要刪除掉所有的低次冪項,忽略掉常數,系數這些次要因素。就和Charles Leiserson 所講的。這個描述,是工程方向的描述,并不是嚴格的數學上的定義。而對像我這樣的小白來說,最大的誤解就是把他當成了數學上的嚴格定義而產生了極大的困惑。
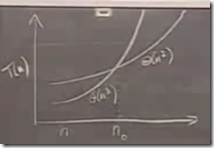
這個是一個相當經典的圖,當n趨于無窮大時,Θ(n3)總能干掉Θ(n2)。不管是同樣的硬件設備,還是不同的硬件設備。只是在不同的設備下,不同的算法下,我們有了一個不同的系數,低次冪項,和常數。但是,我們關心的是他隨著數據輸入長度的變大而產生的增速。當n超過n0時,任何的次要因素都是浮云了。我們就可以說Θ(n3)被Θ(n2)干掉了,即使Θ(n3)的硬件要比Θ(n2)好很多,在一開始的時候效率有多高。
這是一個偉大,cool的概念。是的,他完美的既滿足了我們追求的絕對速度,也能滿足我們追求的相對速度。可以說,這給了我們繼續學習算法的動力。但是,事實上,在實際開發中,我們有時候卻使用那些在學校中認為是效率低的算法。難道這個理論錯了?當然不是,錯的是我們,我們忽略了一個很大的前提,n0。在我們多數開發過程中,很少接觸那些海量數據的運算。我們的運算多數是在一個較少的數據上下浮動,這個也可以說我們的硬件,資金,產品,根本不需要我們整那么大的數據。也就是n0,我們根本達不到。事實上,只要是有腦子的,看到這個圖,在小于n0的前提下,都會做成正確的判斷。但對于剛剛步入IT的廣大學生,卻總是犯下屁股決定腦袋這樣愚蠢的選擇。而這其實,就是做科學和做工程師的最大區別。理論和實踐相互掰手腕的結果。
這幾天,挖老趙的“墳”,找出了這么一篇。寫程序時該追求什么,什么是次要的?里面有一段十分搞笑的代碼,之所以這樣說,是因為我自己也寫過這樣的代碼。想想真是dt啊。回想事發現場,我記得是我看了個什么類似《面試寶典》東東,有一些題考察交換元素,事實上,你可以找到一大堆的,而且是更精妙的去交換2個元素。看到之后,如獲至寶。只要是2個元素要換位置,就用。站在做科學的角度上看,這無可厚非。但是如果站在工程的角度來看。這就是明顯的畫蛇添足。往往花費80%的精力在提高%20的性能上,而不是去花費20%的精力提高80%的性能。這同樣是剛剛步入IT的廣大同學的問題。做科學需要嚴謹,但是在工程方面,考慮的事情非常復雜,多。我們必須要關注在核心,關鍵的部分。這樣才能在有限的資源下,最大的做出東東來。實踐中,沒有任何項目的資源是足夠的。MS,Google都會有資源不足的時候。我們需要學會抓住重點。當然這里并沒有鄙視這些面試問題,事實上,這些問題的背后往往是考察數學思維的基本功,而不是鼓勵大家這么做。就像那個經典的問題,12個小球一架天平。沒有仔細,嚴謹的思考,能夠想到這個東東能和排序問題扯上勾么?神啊,萬惡的功利,給完美的數學模型批了一層邪惡的外套,使我們在追求本質的過程中迷失。
有關n0的問題,不僅在算法設計上,也出現在我們的設計模式之中。《設計模式》這本神書,我是沒看過,也不敢看。但也隱隱感覺到類似“設計過度”的言論。這同樣都是在理論和實踐結合上出了問題。當然,不少理論支持者,肯定會說,那是因為你沒做過那么大的項目。但事實卻是,不管設計多么復雜的,還是多么簡單的,實踐和理論永遠不可能都得到滿足。Windows操作系統可以說是一個我們可見的最大的項目之一了。但是Windows也并不是一個微內核,在內核中也綁定了非常多的“多余”的部分。從理論上看,那無疑會降低系統穩定性,提高維護難度。但是我們卻不能不說Windows是最成功的一套軟件之一(這個之一甚至都可以去掉)。
當然,要想在做學問和實踐找到平衡點。這個無疑是極大的挑戰。只是分析理論,而不實踐,那么永遠不可能成為一個出色的工程師。除非你的目標是成為理論科學家。反過來,如果不理論而只是實踐,不同的是,這個是可以成為一個出色的工程師。所以,這里有一句經典的話。
If you want to be a good programmer, you just program ever day for two years, you will be an excellent programmer. If you want to be a world-class programmer, you can program every day for ten years, or you can program every day for two years and take an algorithms class.
既然算法是如此的重要,那么我們該如何學呢?其實,這是一個很糾結的問題。甚至是一個雞生蛋,蛋生雞的問題。不學算法,你不會了解他,也不會認識到算法重要;認為算法不重要,那么也就不會下功夫去學。這就又回到一開始的那個unknown unknown上了。所以,如果準備學習算法,也就意味著選擇了一條坎坷的路。一開始特別迷茫,但是沒有別的選擇。唯有堅持,放下浮躁,功利的心態,沉浸在數學的世界中才能體會到數學的價值,數學的樂趣。也只有這樣,才能堅持到最后。
當然,能做到這一點的,敢說體會到數學之美的家伙,全世界也沒有幾個人。那么,作為一個普通人,我們怎么才能最大的去提高自己,更好的掌握實踐和科學的平衡點呢?這個問題,我自己也沒有答案。因為我既沒經驗又沒理論。這里只是扯下我自己的理解,可能很偏激。
首先應該研究下劉未鵬的很多博客內容,特別是錘子和釘子。對我這樣的新手來說,武器真的太少了。所以當撿到一個武器往往過于興奮而忽視了這個武器的使用前提,往往殺雞用牛刀,而且還達不到積極的效果。就是因為我們拿到錘子之后,所有東西看上去都像釘子。所以,我們唯有擺正心態,深入了解擁有的武器,并增加更多的武器,見更多的市面,才能坐懷不亂,達到手中有錘,心中無錘的最終境界。
一個稍微實際的例子。對像我這樣的菜鳥來講,大部分都會遇到這樣一個問題。而且困惑很久很久。“堆排序為什么比快速排序在大多數時要慢呢?”事實上,造成這個問題的主要原因(對我)就是,沒有理解明白Θ-notation。那些被忽略掉的次要因素,當然還有更重要的是數學上對概率的薄弱理解。然后我們會再映射出一大堆的數學基礎知識,然后大部分人死在沙灘上(真的,這是我從小以來最大的遺憾,就是沒有學好概率,而造成這個的原因居然是,這些題目初學時往往是用日常用語出題,而由于本人語文太差,總不能理解清楚題意,而對這類題目產生了極大的抵觸,可見小朋友們千萬不要偏科:P)。從科學的角度去,完全可以證明這個問題,但是付出的代價就是沒有碩士以上的數學能力的玩家,沒有機會理解到那個層次。那么,其實我們可以從另一個角度看,直接放到計算機上跑一下就可以了么。是的,我不是科學家,我只需要知道結果就OK了。是啊,好在我們處在一個和諧的世界。讓我們從這個龐然大物中得以解脫,所以,有時,我們需要根據自身情況,放棄一些東西,特別是那些比較能夠通過實驗來證明的東西。
好吧,總不能啥也放棄吧,都放棄了那到底也簡單了。這里,我只能說,我推薦SGI STL。在我看來,這是一個結合了設計模式,理論算法與實踐最好的一個實例。他不僅是開源的,代碼量也不多,命名也算規范,而且還有一本侯捷大師的著作來詮釋,幫助我們理解,而且還能幫助我們具體實踐過程中規避一些錯誤。我們每一個在學校學習的算法,我們都可以在這里找到答案(至少可以用來做作業拿高分對某些特別的女生),而且都會比一般大學講的深刻,事實上,我認為,大學現在的教育為什么覺得無用,不是太難太理論,而是教的太簡單了,簡單到已經沒有用的地步了,從而根本沒有實際意義。(大學聯合培訓機構,是我所見過的,比大學擴招還要搞笑的事情)比如快速排序,SGI STL做了非常多的優化來保證無論在什么時候,都不會退化到n2,在分的過程總是分不好時,采用堆排序。在快速排序到做最后幾步,為了減少開銷而采用插入排序去做哪些馬上就要排好序的部分。而這些策略,并不是憑空想象,都可以在高爺爺的著作中找到理論證明,以及網上的各種論文,前提是你的數學功底足夠(當然這里實踐在前還是理論在前這個實在是沒有討論的意義)。所以,理論不是沒有用,只是自己學的太膚淺。實踐也不是沒有用,只是自己沒有考慮那么多的情況,想的太簡單而已。
當然,這個可能又會引起另一個龐大的問題,“不要重復制作輪子”,不過這個已經大大超出這篇文章的范圍了。我自己的看法是,STL是為了實現最基本的最通用的東東的,而實際過程中,我們往往有自己的特殊性。而這些特殊性是STL不可能設計時都給我們考慮周全的。也就是我們很可能需要擴展,重寫部分以適合我們的需要。當然,現在離這些目標還很遠很遠很遠。
【推薦閱讀】
鄭重聲明:本文版權歸原作者所有,轉載文章僅為傳播更多信息之目的,如作者信息標記有誤,請第一時間聯系我們修改或刪除,多謝。